Converting biometric components into twin control estimates
Turning a nonshared environmental correlation into a twin fixed effect
Sometimes the reason two human traits correlate is that they have shared genetic causes, not that one causes the other. This is a big fly in the ointment for sociology. For example, people from poor families commit more crime: the standard sociologist explanation for this is that this comes from the culture they picked up in their deprived environment. However, it is just as plausible that the heritable traits that predispose to poverty – such as low intelligence and high impulsivity – also predispose to crime, so if you have them you will usually end up with both problems. As it turns out, if you do the proper analysis – a comparison of people from within the same family exposed to different doses of poverty – the latter explanation is correct. In previous posts I said that this is a good way to test the minority stress hypothesis. This hypothesis says that if you are a sexual minority, you are exposed to more stress due to discrimination and this causes poor mental health. But it is also possible that the genetic causes of non-heterosexuality overlap with those of poor mental health. If the minority stress hypothesis is true, the association between non-heterosexuality and poor mental health should be unchanged within MZ twin pairs: even with the same genes, you should be much more stressed and depressed if you are not heterosexual.
The most straightforward way to test shared genetic causes is to test the association within pairs of monozygotic twins. Are richer twins less criminal than their own brothers? Are heterosexual members of the same MZ twin pair better off mentally than their homosexual siblings? These people are genetically identical so the genetic background causes are controlled for. If these were the causes, the association will go away. If, however, there is a causal relationship – poverty causes crime or non-heterosexuality causes poor mental health – the association should persist even within pairs.
There is a less straightforward way to do this though, which is actually the better one. This is the calculation of genetic and nonshared environmental correlations.
When two traits correlate and we have twin data, we can infer if the correlation is because of a genetic or an environmental cause. (Note that we are not talking about the similarity of twins, as in ordinary twin designs, but the correlation of two different traits, measured in samples of people with different degrees of relatedness). If the traits correlate because of their shared genetic backgrounds, the correlation is higher among MZ than DZ twins: if you share more genes, you share more of the traits. If it is shared environmental, the MZ and DZ trait correlations are equal but higher than the population correlation: it’s living in the same family that makes the traits similar. If it is nonshared environmental, the MZ and DZ trait correlations are equal, and also equal to the population correlation. In this latter case, but only then, we have excluded genetic confounding. If one trait is causal for another, their correlation should be equal within pairs of MZ twins and look nonshared environmental in a multivariate twin design. Robert Plomin on this observation in this awesome commentary to one of his own papers:
“However, it was not until the mid-1990s that it was realized that multivariate genetic analysis could be applied to the question of the causality of non-shared environmental effects controlling for genetics. It was not mentioned in the 1987 paper or its commentaries. It took three steps to get to this realization. The first step was to recognize that environmental measures could be treated as phenotypes in univariate quantitative genetic analyses, as discussed in an earlier section on the ‘nature of nurture’. The second step was to incorporate environmental measures in multivariate genetic analyses to investigate the aetiology of covariance between environmental measures and outcomes. As in most quantitative genetic research, this research highlighted the genetic aspect of these results, often finding substantial genetic contributions to the links between environmental measures and outcomes. The third step was to realise that these same multivariate genetic analyses of environmental measures and outcomes estimate the importance of non-shared environment on an outcome independent of genetics and shared environment, using all of the variance within and between identical and fraternal twins. Unlike other analyses of non-shared environment, structural equation model-fitting estimates non-shared environment as a latent variable free of measurement error if the standard assumption is made that error of measurement does not correlate across measures.”
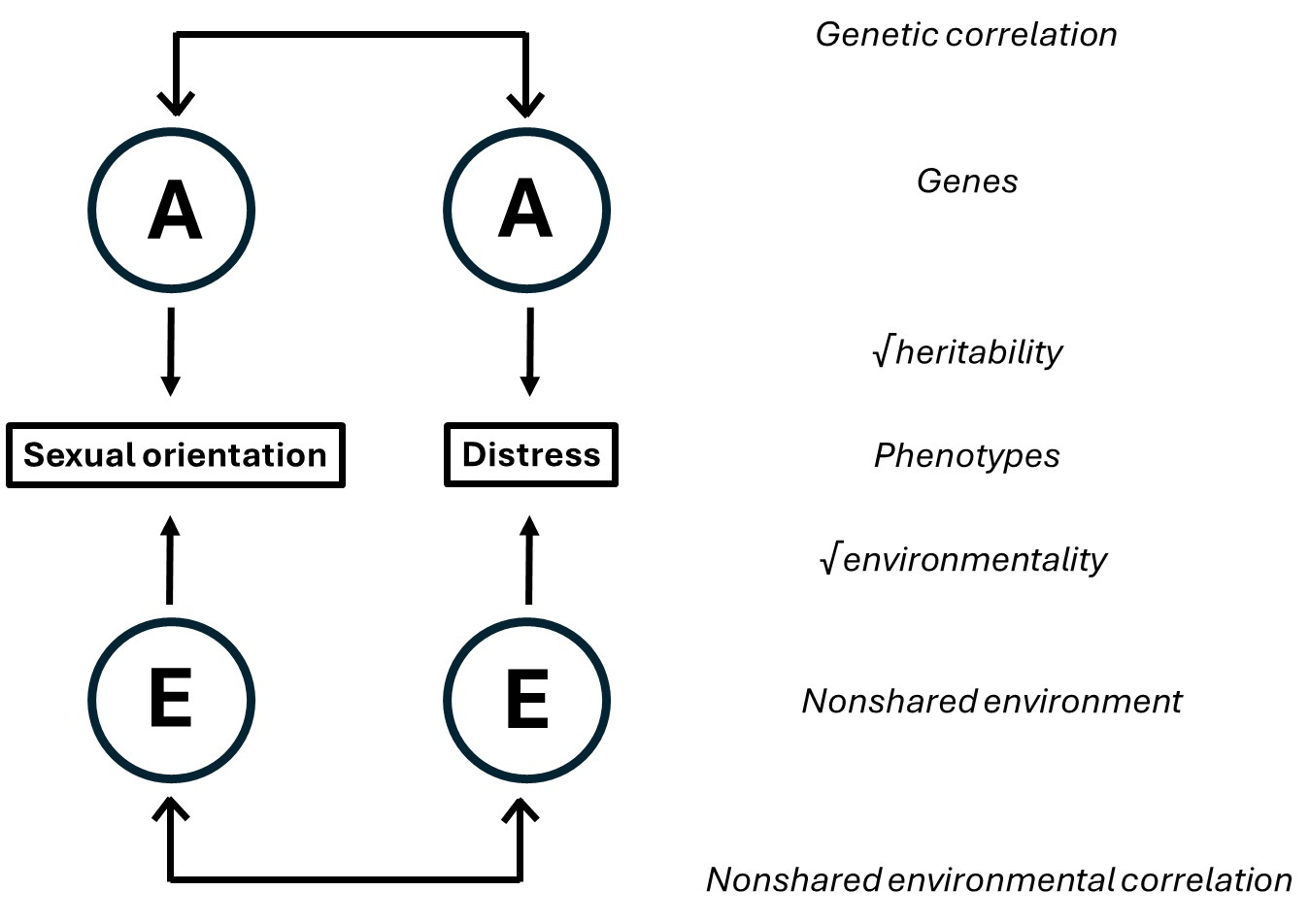
Although Plomin says the two methods are equivalent, he doesn’t elaborate how one can turn one kind of estimate into the other although it’s important pretty straightforward. One can imagine the correlation of two traits – here, sexual orientation and mental distress – to originate from a pathway like this:
Both traits are caused by both genetic and environmental influences. As it happens, both the genetic and the environmental causes overlap somewhat which causes a correlation of the traits. (For simplicity, we model no shared environmental influences.) The total correlation is a sum of these paths:
We take the square root of heritabilities and environmentalities because we the path is the correlation, not the variance explained, between genes/environments and the traits.
Within pairs of MZ twins, the genetic path doesn’t operate, so the estimated correlation is just the environmental path:
If the correlation is all genetic, none of it remains within pairs of MZs. This would falsify any causal claims between the traits. One could convert the resulting rPOP and rMZ estimates to any other effect size to get estimates directly comparable to a normal twin control design. An rDZ estimate would be simply the mean of the MZ and the population estimate.
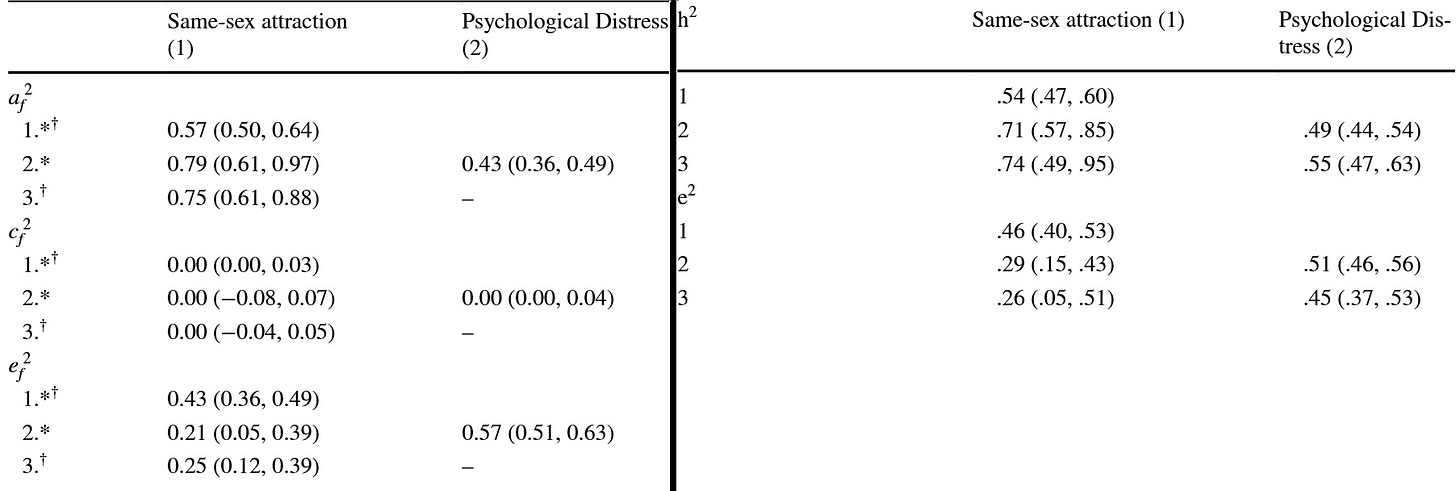
To turn the specific case of the minority stress hypothesis, I’m aware of four papers – Zietsch 2011, Zietsch 2012, and analyses of the UK TEDS and a Finnish twin study by Oginni et al, of which I linked the latest two – which use multivariate twin designs to estimate genetic confounding in the relationship between non-heterosexuality and mental health. The two Zietsch papers neatly provide everything to estimate these equations, and one even derives them. In the two Oginni papers, all we get is this information:
The diagonals are the heritabilities – 57% and 54% - and nonshared environmental determinations – 43% and 46% of same-sex attraction and psychological distress, respectively. The genetic and environmental covariances are reported in numbers that sum to 1: 0.79/0.71 and 0.21/0.29 – in other words, they tell us how much of the full correlation between the traits comes from genetic and environmental sources, but not how much that correlation is. Fortunately, this is reported elsewhere in the papers as 0.25 and 0.3. For example, plugging in the data for the right table we can get:
This is 0.69 but it’s on a weird scale because we didn’t know the proper genetic and environmental correlations, only covariance components that summed to 1. We can make sense of this number if we calculate the estimated MZ correlation from just the second path:
This is 0.26, again on an arbitrary scale. However, the ratio of the two correlations is informative: we can expect that 0.26 / 0.69 = 38% of the total population correlation will persist within MZ twin pairs, and 62% will go away because it was due to genetic confounding. This would mean a within-MZ correlation of 0.11, compared to a population correlation of 0.3. Most of the relationship between non-heterosexual orientation and mental distress is genetically confounded.
This is in line with the fact that MZ correlations are almost twice as high than DZ correlations (0.2 vs 0.13). The authors estimate something similar with a fancy MRDoC path model and get an estimate of the within-MZ effect which is slightly higher (0.19) but 0.11 is within the confidence interval. In the Discussion, the authors bank on the fact that these numbers are not 0 and have the gall to describe their findings like this:
“The causal influence of same-sex attraction on psychological distress demonstrated in the present study is consistent with prior evidence indicating that the phenotypic associations between same-sex attraction and adverse health outcomes are not confounded by correlated genetic and environmental influences”
which is the polar opposite of what their numbers show. Most of the association is in fact genetically confounded.
For the record, in the other Oginni paper, the population correlation is 0.25, of which 0.085 is expected to remain within MZs. In Zietsch 2011, the population correlation between non-heterosexuality and depression is 0.248, rMZ=0.02, in Zietsch 2012, rPOP=0.29, rMZ=0.14.

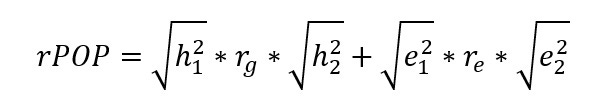


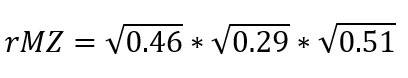
You should remove “genetic” from your first sentence and argument. Even if environmental, the issue is what causes what. Easiest example is random developmental noise, which gets assigned to environment.