Effect size showdown: which correlates stronger?

Parental income and school grades or being unvaccinated and dying from COVID?

Physics is great because its laws are so strong and universal that you can actually use them to recreate the world. If you use physics, you can design a building that is going to actually be 100% like you design it to be and keep standing after hundreds of years. You can land on the Moon. If you understand gravity and some other forces, you can’t just predict how much concrete your construction needs or how much fuel your rocket needs – you will be able to say it exactly.

This is not quite the case for humans who are governed by much less deterministic laws than houses and rockets. Simply put, psychology and related sciences can’t deliver big enough effect sizes. Frank Schmidt et al put the correlation between intelligence and work performance at 0.65. This is an insanely huge effect size – in fact, the largest simple univariate correlation in psychology I can immediately think of – which they arrive at after correcting for various biases. 0.65 is huge as far as a psychology effect size goes, but it’s not exactly house building or moon landing level. Converted to a standardized mean difference, it is d=1.71, which is about the same as the height difference between men and women. You know men are taller than women but you also know that there is quite a bit of overlap, and you can think about the size of this difference: this is about how sure you can be that the smarter person will turn out to be the better employee. Not great, not terrible.

And this is the best correlation! Psychologists have been long disappointed by how low their effect sizes are. This paper by Funder and Ozer is a great summary of the topic. The authors revisit complaints about how bad it is that personality measures can predict behavior at only r~0.4 (sometimes they do better, see e.g. this study of how well personality can be predicted from Facebook likes.) Even 0.4 is great though. In psychology, the mean effect size is about 0.2.

. If you want to get the effect sizes in Cohen’s d – standardized mean differences – in this range you have to multiply these numbers by about 2. Compare this to the much-repeated standard of Cohen himself that 0.5 is a medium effect size and 0.8 is a large one. There are hardly any effects of this size in psychology.

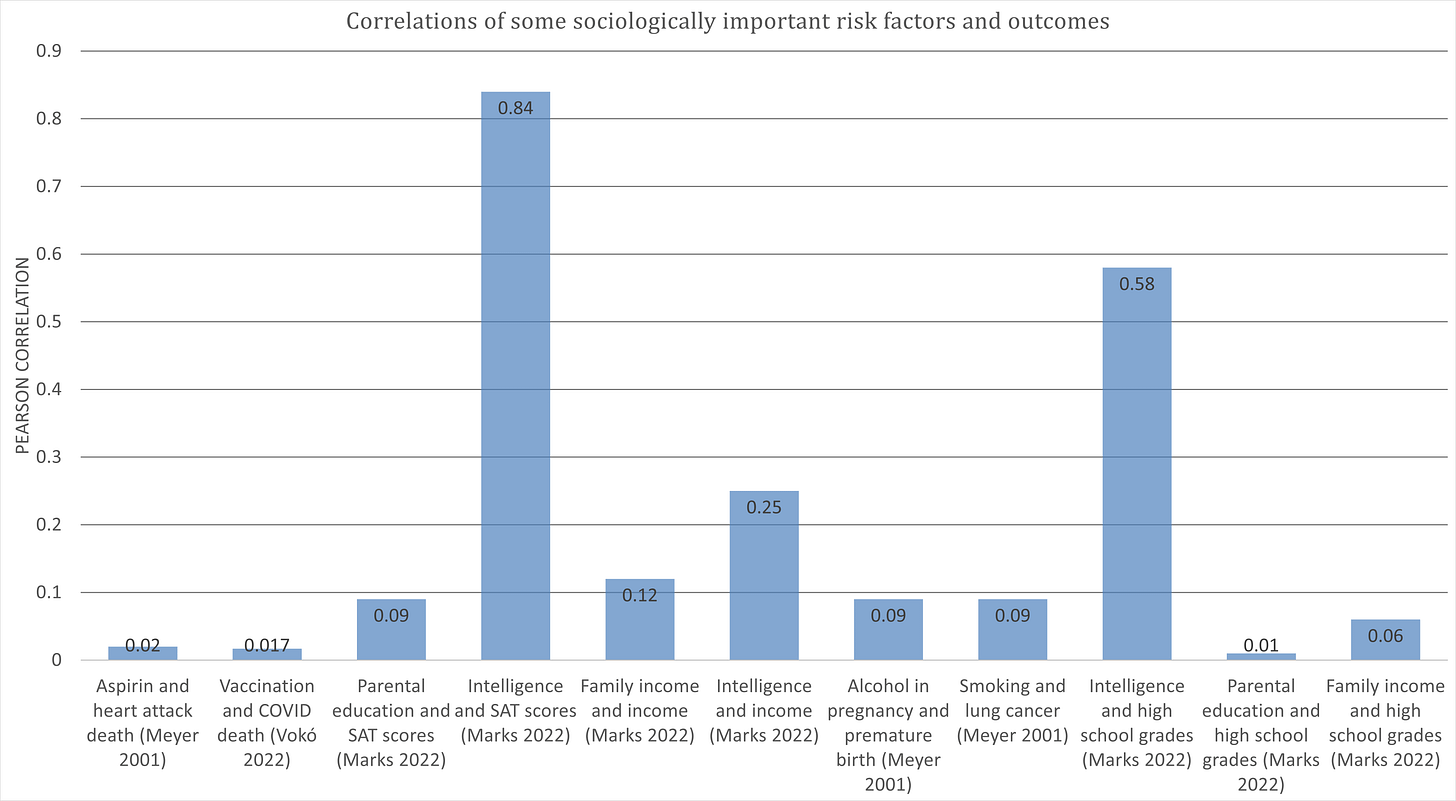
Or anywhere else! This (Meyer et al 2001) is a major troll paper. It starts by examining effect sizes from other fields – most compellingly medicine – to establish a baseline about what we are talking about when we deride the small effects in psychology. Look at this table:

Aspirin against heart attacks – the effect size is 0.02! Antihypertensive medication against stroke – r=0.03! Chemotherapy and breast cancer survival – r=0.03 again! Smoking and lung cancer – r=0.08! Now these are some truly low correlations! Checking at the references, my understanding is that most were converted from risk ratios.

But wait! This reminded me of a paper I wrote about recently, the scandalous Rind et al meta-analysis which found that college students who report having been abused as children are actually not that much worse off mentally. One of the criticism against that paper was that a correlation coefficient is just not a very good measure in these types of studies. The reason for this is that correlation is just a renormed version of covariance (divided by the product of variances). Low variance=low correlation. Now, you must consider that not that while smoking obviously is a risk factor for lung cancer and antihypertensive medication obviously works, the vast majority of people who smoke don’t get lung cancer and most people with or without antihypertensive medications don’t have strokes! This means that in a study like this the vast majority of people will be just marked “doesn’t have cancer/stroke” regardless of what they were doing. The use of rare events like very specific diseases as the outcome reduces variance and this in turn misleadingly reduces correlations. (Ironically, this is not really the case for child abuse. A quite substantial portion of adults report having been abused as children – in the reasonably large and reasonably representative British E-Risk study, for example over 15% reported sexual victimization in the past six years at age 18, almost 20% reported family violence and 15% reported maltreatment. Consequently, the re-analysis of Rind et al found that while the critics were correct in principle, they were incorrect in practice, and the college students reporting having been abused are indeed not disastrously poorly off – however, as I wrote in my previous post, other studies found worse results but it doesn’t matter because this design just doesn’t work to assess the effects of abuse.)

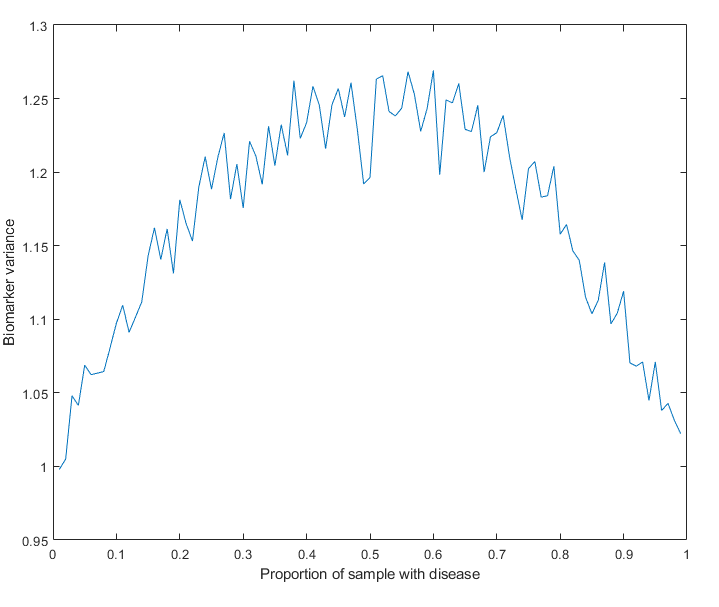
This is not a groundbreaking point to make, but because I just haven’t really seen it laid out like this and because I’m too bad at math to instinctively “feel out” something like this, I had to write a simulation. My MATLAB code is here. My simple simulation works like this. I generate 10k “people” with an “observation” (actually, just a random normally distributed variable). Let’s call it blood marker X. Each “person” has a 0 or 1 label assigned to him – “people” with 1 “have cancer”. Those with “cancer” get an extra 1 SD boost to their X level – not even any noise added. So then, what is the relationship between having “cancer” and having an elevated level of X? It depends on what proportion of the sample “has cancer”.

The actual difference between “cancer” and “no cancer” is actually of course 1. This is accurately recovered even from very small samples when I use Cohen’s d. It is also recovered correctly if I calculate an unstandardized regression coefficient. But if I calculate correlations – technically point-biserial correlations in this case – I’m renorming this by the variance, and because variance is low in an unevenly distributed sample, the correlation is reduced. This is what the variance looks like, not hard to see that this is what drives this problem:

So, point to self and maybe others: don’t use correlations to study rare events!

But what if we stick to the point of Funder & Ozer and the Meyer et al paper and calculate the correlations for rare events – for example, COVID vaccinations and deaths? I’m now turning to Vokó et al 2022 on the efficacy of the vaccines administered in Hungary. This is an interesting paper because it is 1) well written and good to read 2) uses a multi-million person database 3) looks at a very wide range of vaccines, Hungary having been the only country in the EU having the good sense of importing Russian and Chinese vaccines despite muh Putler, muh Winnie the Pooh.

All vaccines were highly effective. Pfizer-BioNTech was 83.3% effective against infection and 90.6% effective against mortality. Sputnik was easily the best with 97+% effectiveness against both, and even the supposedly weakest Chinese vaccine was 68.7% effective against infection and 87.8% against mortality – interestingly, these estimates change quite a bit after adjustment for age, sex and calendar day, not always in the same direction and in spite of the fact that they are all quite precise.

With Pfizer, there were 12980 deaths in the unvaccinated and 280 in the vaccinated. That’s a huge difference! But we need to consider that this is an apples to oranges comparison: there were much more unvaccinated people than people vaccinated with this particular type of shot, and actually it’s not even ‘people’ we are talking about, it’s person-days. This is important because in a normal vaccine trial you would vaccinate N people, give a placebo to another group of people (probably reasonable close to N in number) and wait to compare them. But here, people could jump between ‘treatment arms’: for example, if you were unvaccinated from January 1 to January 30, vaccinated on January 31, you contributed 30 ‘unvaccinated’ person-days to the study, and afterwards, you started contributing ‘vaccinated’ days. (Actually, people were considered unvaccinated up to 7 days after their second shot in this study.) So we cannot do anything with the raw cases or deaths, only the ratios per person day. These look like this:

The unadjusted vaccine efficacy can be easily recovered from these numbers: 1-(0.4/1.56)=0.746 for Pfizer (reported efficacy: 74.3%), 1-(0.6/1.79)=0.665 (reported efficacy: 66.1%) for Sinopharm. So, what is the correlation between ‘being vaccinated against COVID’ and ‘not dying from COVID’? Depends on the mortality rate!

Technical details: I am basically simulating a Phase III vaccine trial here. I evenly split the sample of N=10k, half were vaccinated, half were not. For simplicity, we assume that everybody gets infected eventually. Vaccination status doesn’t change: you are either vaccinated or not. Mortality rate was simulated between 0.0001 to 0.9999, and this was multiplied by 1-efficacy to simulate mortality in the vaccinated. The effect size I’m calculating is literally the Pearson correlation between binary vaccination status and binary ‘being dead’ status – this is a legal thing to do, it’s called the phi coefficient, although I am cheating a little by doing this. For two binary variables, a more standard method would be a tetrachoric correlation. However, we started with Pearson correlations so let’s finish with them.

You can see that the deadlier the disease, the more effective the vaccine looks. There is no reversal with high mortality. Why? Because with vaccines this effective, a lot of people survive even if mortality is 99.99% without vaccination, so survival doesn’t become nearly as rare as death was at a low mortality rate. In the most extreme simulation of assumed 99.99% mortality, it so happened that nobody in the unvaccinated sample survived, but there were only 1352 deaths out of 5000 in the Pfizer-like vaccinated (efficacy=74.6%, so death rate only about 25% of the original) sample.

So what is the best estimate for a correlation between vaccination status and COVID death? Obviously this depends on the mortality rate of COVID. If we stick to this study, mortality rate is very hard to calculate because there is no given number of people here who are ‘vaccinated’ or ‘unvaccinated’: vaccination status can change. There were 1497011 people vaccinated with Pfizer, and dividing vaccinated person-days by this number tells you that they were followed up by an average of 45 days (remember, counting started 7 days after their second dose!). In these 45 days, 280 people, about 0.018% died of ‘COVID-19 related causes’ – at the height of the epidemic this may have been a quite liberally applied category. Remember, this is not a case or infection fatality rate, but a population fatality rate! Anyway, plugging this number into the equation (after simulating 1M cases now, because hardly anybody dies out of 10k) returns – drum roll – r=-0.017 for the Pfizer vaccine and r=-0.01 for Sinopharm. Cohen’s d is is a respectable -0.49 for Sinopharm and -0.58 for Pfizer. It is somewhat odd to calculate a Cohen’s d for binary data though, a more standard measure would be the odds ratio or risk ratio. In this case, the odds ratio turns out to be 0.26 and the risk ratio turns out to be 0.64, both are highly significant and quite respectable numbers. The more standard tetrachoric correlation is -0.38 for Sinopharm and -0.47 for Pfizer – this is much higher than the phi correlation! However, as MATLAB doesn’t have a built-in function for tetrachoric correlations (lol), I implemented some formulas I found on the internet. These seem to work reasonably well and they all return similar results, but when I calculate the same with the polychor() function in R, the value is only about half this much, which sounds more believable for me than both my values and the phi coefficients. But polychor() uses a much more complex method. Let this be a cautionary tale about effect size comparisons.

This reminds me of the recent paper by Gary Marks, in which he basically summarizes and replicates The Bell Curve with recent data from the NLSY79 and NLSY97. The question is: how well do family characteristics predict where you end up in life (any sociologist worth their salt would tell you ‘very’), and how does this change if you add cognitive ability to the equation? The short answer is the same as in The Bell Curve: it’s basically all just g. Social status runs in families because intelligence is heritable, so smart people create successful families and beget smart children who, once they have grown up, also become successful. The family environment does zero to very little to complement or modify this effect. (Personally, I lean towards ‘very little’ rather than ‘zero’, for reasons I will probably once describe.)

A little longer, by the numbers summary looks like this (beta coefficients of four predictors on a series of outcomes):

I report only the standardized betas from the last model, which considers all three or four predictors. This is the most informative because 1) in can be considered as a correlation coefficient (net of the other predictors) 2) it is on the same scale of all variables. You can trust these numbers for what they say: what you see here is not how much higher SAT scores kids of richer parents have, but how much higher scores kids of richer parents with the same IQ have. Years in education (for the person we are studying, not his parents) are also used as a predictor in some models. Unfortunately, the models using wealth as the outcome don’t report easily interpretable, correlation-like betas, only unstandardized regression coefficients. I just said these are preferable because they are not affected by how much variance there is in the data, but a drawback they have is that you can’t easily make sense of their scale of measurement. I added an asterisk wherever there was a significant effect, regardless of how significant.

The results are the usual: cognitive ability is the best predictor of everything (except occupational attainment and almost income, which are strongly influenced by how much you studied, even net of cognitive ability). This is much studied and probably a signaling effect which peters out after about age 30: employers look for not just smart, but also diligent, organized, obedient and not too weird people and having attended a lot of formal schooling is a good signal of these traits. It is expensive to obtain, but then again, it’s not the employer who pays for it! Parental education and income take not a second, but a third or fourth seat behind cognitive ability, with the possible exception of educational attainment – some parents might just be more prone to send kids to more school, or maybe parental education indexes some genetic trait other than intelligence which contributes to a similar outcome in the offspring. Interestingly, net of family income, the kids of more educated people make significantly less money – one would think of strange, overeducated humanities graduates having slacker hippie kids.

The reason these results are relevant here is because we can contrast these betas with the coefficients we have seen so far. What is stronger, the effect of vaccination on COVID mortality, parental income on kids’ SAT scores, taking tamoxifen on breast cancer mortality or smoking on lung cancer? Here is a quotable, shareable, tweetable, semi-serious illustration of this:

I don’t fully endorse this message that many medically important correlations are so tiny, because using Pearson correlations is just not appropriate in many of these contexts. But the overall message stands: many correlations we take for granted and obvious are actually very weak compared to the correlations discovered by personality psychologists and especially IQ researchers. If you want to find the most physics-like human science, don’t look at medicine, look at IQ research.